Warum DSP-Controller unterschiedlich klingen

Warum klingen DSP-Controller von verschiedenen Herstellern unterschiedlich, wenn man sie mit den gleichen PEQ Settings einrichtet? Stellt man diese Frage fünf verschiedenen Tonleuten, bekommt man mit Sicherheit zehn verschiedene Antworten. Meist landet man nach einer viertel Stunde Diskussion im Bereich esoterischer Mystik.

Von Bodo Felusch

Auf der einen Seite sind es genau diese Diskussionen, die den Job so spannend machen – auf der anderen Seite kann man nicht einfach akzeptieren, dass so ein sensibles Nadelöhr wie Systemcontroller extreme Toleranzen hat. Sie sind das letzte Glied vor dem Lautsprecher und seiner Endstufe und entscheiden maßgeblich über den Klang und die Lebensdauer des Systems.

Über den Klang und die persönlichen Präferenzen von Equalizern in Mischpultkanälen kann man streiten und sie je nach Programm auch gezielt wählen, für die Auswahl von Systemcontrollern sollten solche Parameter jedoch keine Rolle spielen. Ihre Aufgabe ist klar: Schutz und lineare Übertragungsfunktion im Sinne des Lautsprecherherstellers zu gewährleisten.

Tatsache ist: Wenn man Controllter verschiedener Hersteller mit den gleichen Daten beschickt, erhält man unterschiedliche Ergebnisse. Das führt dazu, dass Systemtechniker einzelne Exemplare geradezu heroisch vergöttern und Hersteller vermehrt zu geschlossenen Systemlösungen tendieren.

Dass sich die Wertschöpfungskette nebenbei um Endstufen und Controller erweitert, soll für uns Anwender erstmal keine Rolle spielen, schließlich überwiegen auch für uns die Vorteile, wenn ein System auf der ganzen Welt gleich klingt.

Wer immer noch glaubt das Geräte unterschiedlicher Hersteller nur verschieden klingen, weil Gurus in den R&D-Abteilungen Geheimwissen über A/D- und D/A Wandler haben, sehe sich die folgende Abbildung an :

Abb 1: Vier verschiedene EQ AU Plug Ins mit den gleichen Q Werten. Die Gain Werte wurden zur besseren Übersichtlichkeit angepasst. (anklicken vergrössert)

Selbstverständlich findet man Qualitätsunterschiede bei Verarbeitung, Wandlern und Rechenalgorithmen. Anders kann man der Tatsache, das Geräte in unterschiedlichen Preisklassen notwendig sind, auch nicht gerecht werden. Ebenso selbstverständlich führen diese Unterschiede auch zu Klangunterschieden. Diese möchte ich hier aber weder bewerten noch erörtern.

Konzentrieren wir uns auf den wesentlichen Faktor, nämlich die Definition der Bandbreite. Wie wir in der obigen Abbildung sehen, scheint diese – anders als wir in der Schule gelernt haben – eben nicht genormt zu sein. Schauen wir uns das Thema also mal genauer an.

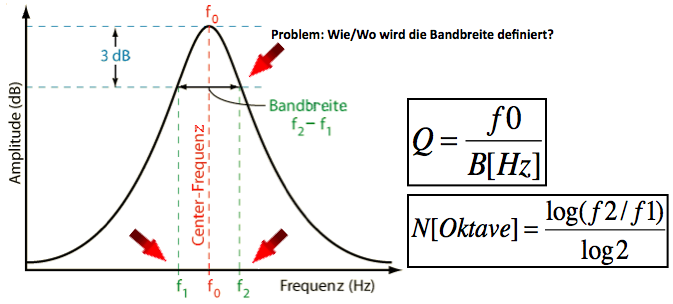Abb 2: Standard Schulbuchmeinung zur Definition der Bandbreite von PEQ und Umrechnung von Q & BW

Diese Abbildung kennen wir alle, sie gaukelt uns vor, die Bandbreite von parametrischen Equalizern ist am -3dB Punkt definiert und kann mithilfe der Formeln einfach hin und her gerechnet werden. Der Vorteil liegt darin, dass Prüfungsergebnisse von Klausuren eindeutig korrigiert werden können und Techniker mithilfe von Exel-Tools Werte für Q-Faktoren in Bandbreite pro Oktav umrechnen können.

Mit richtigen bzw. eindeutigen Ergebnissen hat das in der Praxis leider nichts zu tun, sonst käme es wohl kaum zu Ergebnissen wie bei den obigen AU Plug Ins. Absolut betrachtet ist die ganze Sache auch kein Problem „…stell doch einfach den EQ so ein bis es passt“. Spätestens wenn wir die dazu passenden Herstellerangaben ablesen, stellt sich aber die Frage nach dem Sinn: Warum werden Angaben überhaupt gemacht, wenn sie nicht austauschbar sind. Schließlich möchte ich in der Praxis den Wert von Gerät A in Gerät B übertragen, OHNE dabei Toleranzen in der Übertragungsfunktion zu verursachen.

Zurück zu dieser einfachen Definition: am -3dB Punkt stellen sich zwei Fragen:

1. Was ist mit Gain Werten kleiner -3dB?

2. Was ist mit positiven Gain Werten – Ist das Verhalten bei Cut und Boost zwingend gleich?

Sehen wir uns zunächst einmal an, wie ein parametrischer EQ üblicherweise konstruiert wird.

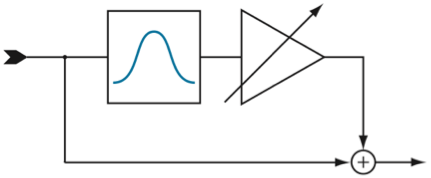Abb 3: Konstruktion eines PEQ mittels eines Bandpasses

Wir schicken das Signal durch einen Bandpass 2. Ordnung und mischen es dem Original zu. Der Pegel der Zumischung ergibt den Filter Gain und für Absenkungen wird die Polarität des zugemischten Signals gedreht. Das Ergebnis ist dann folgende Übertragungsfunktion.

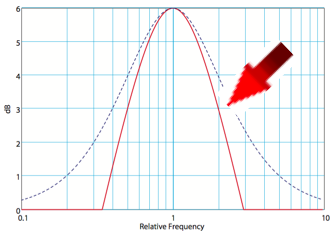Abb 4: Übertragungsfunktion des Bandpasses (rot) und des resultierenden PEQ (blau gestrichelt)

Schauen wir uns den -3dB Punkt in dieser Abbildung an, dann wird klar, dass die gestrichelte Linie (welche den resultierenden parametrischen EQ darstellt) breiter ist als die des Bandpasses selbst. Dies ist der Tatsache geschuldet, dass die Flankensteilheit des Bandpasses bzw. seine Ordnung nicht unendlich hoch ist. Was wir uns allerdings merken können ist, dass die Bandbreite eines Bandpasses immer am -3dB Punkt definiert ist. Das wird sicherlich jeder Nachrichtentechniker genauso sehen.

Leider trifft diese Definition eben nicht zwingend für alle parametrische EQs zu, das ist ein Konstrukt, das Toningenieure für sich geschaffen haben.

Hier ergeben sich die ersten beiden Definitionsmöglichkeiten:

Definitionsmöglichkeit 1:    (Bandpass Bandbreite unkompensiert / Bandpass Q)

1. Die Bandbreite des zugrundeliegenden Bandpasses wird einfach als Definition für die Bandbreite des PEQ´s genommen. Die Tatsache, dass die resultierende Bandbreite zwingend breiter ist, wird ignoriert.

Definitionsmöglichkeit 2 :   (Bandpass Bandbreite fix kompensiert)

2. Zusätzlich wird ein fester Offset zur Fehlerkompensation definiert, dieser stimmt dann näherungsweise für einen Gain Wert der PEQ.

Nun kennen wir zwei Möglichkeiten, eine generell ungenaue und eine relativ ungenaue, sobald man vom Gain-Wert abweicht, anhand dessen man den Offset definiert hat. Außerdem haben wir bisher die -3dB Problematik des Bandpasses komplett ignoriert. Das führt uns jetzt zu den nächsten zwei Definitionsmöglichkeiten die zum Ziel haben kleinere Gain Werte besser zu berücksichtigen …es wäre nicht gerade zielführend die Toleranzen nur bei +/-10dB Gain Werten zu minimieren.

Definitionsmöglichkeit 3 + 4:

Zunächst definiert man, dass die Bandbreite nicht am -3dB Punkt sondern am 3dB vom Peak Punkt definiert ist.

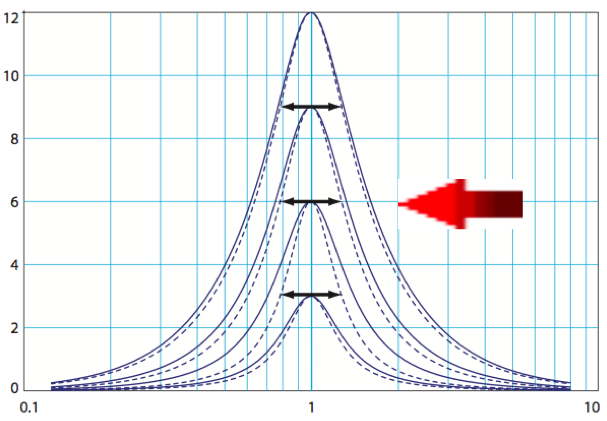Abb 5: Bandpass Q und 3dB Hybrid Methode (gestrichelte Linie)

Definitionsöglichkeit 3:    (3dB Hybrid Methode  …gestrichelte Linie)

Für Gain Werte kleiner 6dB wird die Bandbreite anhand der Hälfte des Filter Gain definiert. Bei Gain Werten größer 6dB geht man über zur „normalen“ Definition am Bandpass.

Definitionsmöglichkeit 4:  (db/2 Methode)

Diese Methode definiert die Bandbreite grundsätzlich so, als wäre das Filter-Gain nur die Hälfte, was zu engeren Filtern bei höheren Gains führt.

Jetzt kennen wir vier Möglichkeiten, die Bandbreite eines parametrischen Equalizers zu definieren. Sie alle bauen auf die Bandbreite des zugrunde liegenden Bandpasses auf und kompensieren die entstehenden Toleranzen mehr oder weniger. Doch was ist mit dem Cut/Boost Verhalten? Verhalten sich parametrische Filter die auf „zugemischten“ Bandpässen basieren immer gleich? Egal ob wir anheben oder absenken?

Cut vs. Boost

Wie wir wissen, wird ein Cut-Verhalten durch Invertierung bzw. Polaritätsumkehr des zugemischten Bandpasssignals erzeugt. Wie selbstverständlich geht man davon aus, dass die Bandbreite gleich bleibt, wenn man die Finger vom Q läßt und von -5 auf +5dB Gain dreht. Bis auf ein paar (meist teure) Ausnahmen, ist das ja auch so. Wenn man bedenkt, das die Bandbreite des Bandpasses am -3dB Punkt definiert ist und es beim Bandpass gar keinen +3dB Punkt gibt, dann sollten wir also erwarten, dass Cut-Filter naturgemäß enger sind als Boost Filter. Genau das passiert, wenn man keine Kompensation des Cut/Boost Verhaltens vornimmt.

Definitionsmöglichkeit 5:   (asymetrische Filter / Constant Q Filter*)

Die Bandbreite/Q-Faktor ist unabhängig von Cut oder Boost konstant definiert. Der zugrunde liegende Bandpass hat unabhängig von Cut oder Boost die gleiche Bandbreite bzw. Güte.

Abb 6: asymetrische Cut/Boost Filter basierend auf konstanter Bandpass Bandbreite (anklicken vergrössert).

Definitionsmöglichkeit 6   (symetrische Filter / variable Q* / reciprocalpeak-dip)

Das Cut/Boost Verhalten wird symetriert durch Anpassung der Bandpass Bandbreite. …zwei identische Filter, einer Cut einer Boost, heben sich phasenlinear gegeneinander auf (Anklicken vergrößert).

Abb 7: symetrische Cut/Boost Filter basierend auf variabler Bandpass Bandbreite (anklicken vergrössert)

Benutzung der Begriffe Constant Q* & Variable Q*

OK, es gibt also zwei weitere Möglichkeiten, um sie mit den ersten vier Methoden zu kombinieren: Symmetrisches oder asymmetrisches Cut/Boost Verhalten. Doch die Verwendung der Namen kann auch wieder zu Verwirrung führen. Ist für den Konstrukteur vielleicht das resultierende asymmetrische Verhalten ein „konstant Q“ Filter da der Bandpass eine konstante Bandbreite hat. So denkt vielleicht die Marketing Abteilung genau andersherum und sagt „konstant Q“ bezieht sich auf das Cut/Boost Regelverhalten.

Andere Hersteller sagen vielleicht „variable Q“ heißt bei uns db/2 Methode und führt zu engeren Filtern bei höheren Gains. Wieder andere Hersteller machen es ein bisschen anders und nennen Ihre Filter „adaptive Q“ – Letztendlich muss man die Herstellerbezeichnung hinterfragen, was jedoch voraussetzt, dass dieser sie auch beschreibt. Ich reduziere die Möglichkeiten bei der Bezeichnung einfach auf die zwei nahe liegenden:

Möglichkeit 1 (Entwicklersicht):

Bezogen auf das techn. Verfahren -> Contstant Q = asym. Filter

Möglichkeit 2 (Anwendersicht):

Bezogen auf das Ergebnis-> Contstant Q = sym. Filter

Wer macht was?

Leider dokumentieren die Hersteller in den seltensten Fällen Ihre Definition der Bandbreite. In der Praxis haben sich aber die oben beschriebenen Methoden bewährt, sie sind die Basis für das was wir am Markt vorfinden.

Es lässt sich also relativ einfach messtechnisch herausfinden, welche Methode der Hersteller anwendet. Bei einigen Produkten kann man die Methode/Definition auch umschalten, wie z.B. beim BSS Soundweb. Bei den Recherchen zu diesem Artikel bin ich auf folgende Ergebnisse gestoßen:

XTA | TOA | Ashley | Rane | EAW:

Symmetrisches Cut/Boost Verhalten + Definition der Bandbreite am -3dB vom Bandpass Punkt durch Variation des Q Faktors des zugrunde liegenden Bandpasses.

BSS (Omdidrive, Soundweb) | Mediamatrix:

Symmetrisches Cut/Boost Verhalten + Definition der Bandbreite am -3dB vom Peak Punkt durch Variation des Q Faktors mit der 3dB Hybrid Methode

Umrechnung und Transfer von Herstellerangaben

Hersteller von „offenen“ Systemen veröffentlichen Prozessor Settings für ihre Lautsprechersysteme. Im Optimalfall geben sie den Hersteller/Typ der Prozessoren an, für den die Settings passen. Dem Anwender obliegt es nun, diese Angaben mittels verschiedener Exel-Tools für andere Prozessoren umzurechnen/konvertieren.

Hat der Hersteller seine ursprüngliche Angabe nicht dokumentiert, haben wir hier schon die erste Fehlerquelle. Die zweite Fehlerquelle liegt dann beim Anwender, dem die Wahl der richtigen Konvertierung obliegt. Im schlimmsten Fall kumulieren sich hier die Fehler.

Abb 10: Hersteller Spec Sheet Angabe für EAW JFX260 und Umrechnungsergebnisse mit verschiedenen Tools. (Die Angabe im roten Kasten ist der umgerechnete Q Wert für Lake Raised Cosine Equalisation, was für Lake Processing aufgrund der generell anderen Berrechnungsmethode immer erfolgen muss!)

Praktisches Beispiel

Wie sagt ein Kollege immer so schön „…Du kannst das schon so machen, aber dann ist es halt Kacke“. Schauen wir uns nun an was in der Praxis passiert, wenn wir beim o.a. Beispiel der EAW JFX260 bleiben und diesen mit einem EAW LA400 Subwoofer kombinieren. Ohne das Wissen wie man Q/BW Angaben theoretisch korrekt umrechnet und anwendet können verschiedene Ergebnisse erzeugt werden.

Als Systemprozessor dient in diesem Beispiel ein Lake LM44, der aufgrund der verwendeten Berechnungsmethode (Raised Cosine Equalisation) spezieller Aufmerksamkeit bedarf. Der Hersteller EAW liefert in seinen Processor Settings Spec Sheets Angaben für Q und Bandbreite, ohne die Definitionsmethode zu dokumentieren. In dem EAW Exeltool liefert er in der Version von 2007 die fehlende Information. EAW gibt in den ProzSettings Sheets den Q Faktor und die Bandbreite für Bandpass Q Definition an und ermöglicht die Umrechnung für BSS und Mediamatrix mit der 3dB Hybrid Methode.

Die erste Fehlerquelle für den Anwender von Lake Processing liegt nun in der Annahme, er könne die Bandbreiten Angabe aus dem Spec Sheet direkt verwenden. Das ist falsch! Der Q-Wert muss für Lake Processing speziell umgerechnet werden, was in diesem Beispiel zu einer Bandbreite von 1,9 statt 1,27 bei einem exemplarischen PEQ führt.

Abb 11: Lab.gruppen LM44 Übertragungsfunktionen für EAW JFX260 BI-Amped + LA400 (anklicken vergrössert).

Hier stellt sich jetzt natürlich die Frage, ob EAW möchte, dass das Lake Load Library Preset 2-3dB weniger HF hat? Man sollte meinen, dass ein Lake Loadlibrary Preset, das vom Hersteller kommt, den Lautsprecher bestmöglich nach dessen Philosophie betreibt, was die Frage nach der „echten“ Referenz aufwirft. Also schauen wir uns das Lake Loadlibrary Preset nochmal gegen den EAW UX8800 Systemprozessor an, der im Gegensatz zum Lake FIR gefilterte Focused Presets beinhaltet.

Abb 12: Übertragungsfunktionen für EAW JFX260 BI-Amped + LA400. Lab.gruppen LM44 Load Library v3.1 (rot) vs. EAW UX8800 Greybox (weiss) (anklicken vergrössert)

Hier sind jetzt so extreme Unterschiede zu sehen und zu hören, dass man sich fragen muss, ob EAW bei den Focused Greyboxen Presets eine neue Philosophie verfolgt oder es sich schlicht und einfach um einen Marketinggag für Focused Greyboxen handelt.

Unumstritten ist, dass die Focussed Technology, die David Gunness für EAW entwickelt hat, in einer NT56 zum Beispiel hervorragend funktioniert. Der Lautsprecher hat eine absolut lineare Übertragungsfunktion und klingt dabei genauso hervorragend wie er messtechnisch aussieht. Das gleiche gilt für eine non-focused betriebene JFX260, die wahlweise Fullrange passive oder BI-Amped betrieben absolut Flat getuned ist. Aus der Reihe tanzt die Focused Greybox, die subjektiv irgendwie mehr Mitten und Höhen hat und, um das gehörmäßig zu kompensieren, eine kleine LF Beule dazu bekommen hat. Das UX8800 Greybox Setting ist zwar FIR focused, was das Lake Loadlibrary Preset natürlich nicht ist, von daher sind Unterschiede in der Übertragungsfunktion natürlich zu erwarten, aber die tonale Abstimmung sollte der Herstellerphilosophie folgen und nicht gravierend anders klingen.

Jetzt kann man natürlich sagen, alles was nicht focused ist sind alte MX Presets und keine Referenz mehr, die echte Referenz kann nur das aktuelle Greybox Setting sein. In dem Fall sehe ich das einfach anders, ich mag an EAW Presets und Lautsprechern die lineare Abstimmung …der Lautsprecher soll das rausgeben was ich reintue und für den Sound bin ich zuständig. Das EAW focused Greyboxsetting kann übrigens direkt in eine PLM Endstufe oder eine Powersoft DSP Endstufe geladen werden. Ohne das jetzt zu bewerten stellt sich aber die Frage: Was ist die „richtige“ Referenz?

Autor: Bodo Felusch, dieser Artikel erschien ursprünglich auf www.felusch.de